개요
- 동족좌표계? Affine Space? 동차좌표? Homogeneous coordinate?
- 왜 1,4 행렬로 3차원상의 점과 벡터를 표현하나요?
1. Affine Space(동족 좌표계)란?
어파인(혹은 어핀) 스페이스는 다른 말로 동족 좌표계 라고도 하며, 쉽게 말하면 벡터와 점을 같은 것으로 간주하는 공간이다.
3차원 공간에 (1,2,3)로 표현되는 무언가가 존재한다면, 이것은 1,2,3 위치의 점이라고 말할 수도 있고, 원점에서부터 1,2,3으로 향하는 벡터라고도 볼 수 있는 것이다.
이렇게 점과 벡터를 함께 표현하게 되면, 점과 점의 뺄셈으로 벡터를 얻을 수도 있고, 점에 벡터를 더해 다른 위치의 점을 구할 수도 있다.
그러나 그냥 똑같이 표현하면 이게 점인지 벡터인지 알 수가 없기 때문에 이 둘을 다르게 표현하기 위해 사용하는 것이 동차 좌표이다.
2. 동차 좌표
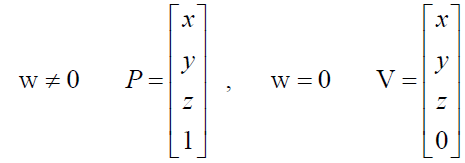
결론부터 말하면 3차원 상의 점과 벡터를 3개의 요소가 아니라 4개의 요소로 표현하게 되는 것이 동차 좌표의 특징이다.
(n차원 상의 점과 벡터를 n+1개의 요소로 표현하는 방식을 동차 좌표라고 하지만 3차원을 가장 많이 씀)
마지막 요소가 0이면 벡터, 1이면 점이다!
사실은 0이 아니면 전부 점인데 이게 1이 아니라 2일수도 있고 5일수도 있고 3/4일수도 있다.
3. 왜 그렇게 될까?
사실은 점과 벡터를 다르게 표현하기 위해 4번째 요소가 생김에 따라서 이것은 4차원으로 바꿔서 생각할 수 있다!
3차원 공간에 동차좌표 (1,2,3,1) 이라고 표현된 점이 하나 있을 때 사실 이것은 4차원으로 보면 원점에서부터 (1,2,3,1) 점을 잇는 직선상의 모든 점과 같다!
이 직선상 모든 좌표는 곧 3차원 동차좌표 상 1,2,3,1과 동일한 점으로 볼 수 있는 것이다
그러니까 (1,2,3,1) == (2,4,6,2) == (10,20,30,10) == ... 라고나 할까!
그래서 마지막 요소를 1로 만들어 주도록 4개의 수에 같은 수를 곱하거나 나누는 것을 동차화 과정이
라고 한당!
예를 들면 2,4,6,2 라는 점이 있을 때 이것은 사실 2로 나눈 (1,2,3,1) 로 동차화 과정을 거친것이 실제 좌표가 된다.
'computer science > 3d graphics' 카테고리의 다른 글
| 왜 정규화 벡터를 사용하는가 (0) | 2021.07.26 |
|---|---|
| OBB (Oriented Bounding Box)와 AABB (Axis-Aligned Bounding Box) (15) | 2021.07.26 |
| 컴퓨터 그래픽스 렌더링 파이프라인의 개요 (0) | 2021.07.26 |
| 짐벌락과 오일러 각 (gimbal lock, euler angles) (0) | 2021.07.26 |



댓글