개요
- 오일러 각이란?
- 짐벌락이란?
- 짐벌락은 왜 생기나?
1. Gimbal 이란?

출처 - [http://ko.wikipedia.org/wiki/%EC%A7%90%EB%B2%8C]
이것이 바로 짐벌이다.
위키에는 단일 축으로 물체가 회전하도록 중심축을 가진 구조물이다. 라고 되어있다.
그림에서는 roll pitch yaw 세개가 바로 그 단일축이다.
자세히 보면 각각의 고리는 본인이 가진 축을 기준으로만 회전한다.
각각의 고리는 각자의 단일축으로 회전하는데도 불구하고 파란 고리가 축에 관계없이 모든 방향으로 회전하는 것처럼 보이는 이유는 바로 고리들이 서로 연결되어있기 때문이다.
고리가 다른 고리에 자식으로 붙어있는 관계이기 때문에 각 축은 서로 종속적이다.
실제로 이러한 구조물을 선박에서는 자이로스코프, 나침판, 난로, 그리고 컵홀더까지
전후좌우로 흔들리더라도 수평을 이루도록 할 때 많이 쓰인다고 한다.
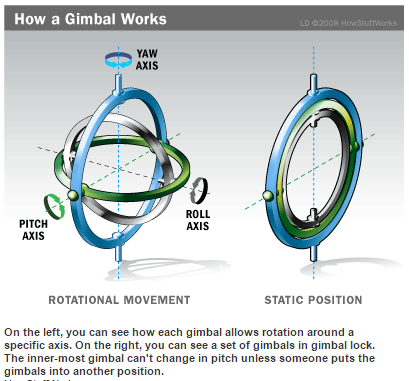
출처 - [http://science.howstuffworks.com/gimbal1.htm]
[왼쪽 그림에서 각각의 짐벌은 특정한 축을 기준으로 회전하도록 되어 있습니다.
오른쪽 그림에서 짐벌들은 짐벌락 상태에 있습니다.
가장 안쪽에 있는 짐벌은 짐벌들을 다른 상태로 돌려놓지 않는 이상 roll 축으로 회전할 수가 없습니다.]
오른쪽 그림을 잘 보면 회색 회전축이 사라져 있다.
왜 이런 현상이 발생하는 것일까?
2. 오일러 각이란
오일러 각이란 오일러가 도입한 강체(rigid body)의 회전 시스템이다.
(강체란 힘을 가해도 모양이 변하지 않는 그러니까 평행이동과 회전만 가능한 물체라고만 생각해두자)
어떠한 강체가 3차원 공간 상에 존재한다고 해보자.
이 강체를 수학적으로 표현하기 위해서는 위치(position)나 방향(rotation)을 정의해야만 한다.
위치는 x,y,z 좌표를 통해 (0,0,0)라고 쉽게 정의할수 있다.
하지만 방향은 어떻게 정의하면 좋을까?
xyz 세축을 기준으로 회전하면 되지 않을까?
라고 오일러가 제시한 것이 오일러 각 시스템이다.
오일러각은 xyz 세축에 익숙해진 우리에게는 매우 직관적이다
(그러나 이 오일러 각을 통한 회전에는 심각한 문제가 있는데 그게 짐벌락이다.)
결론적으로 오일러 각이라는 것은 3차원상의 강체의 방향과 회전을 정의하기위해 만들어낸 시스템이다.
3차원 공간에 존재하는 어떠한 강체를 회전하고 싶으면 세개의 축을 통한 회전으로 표현할 수가 있다.
대신 회전을 할 때에는 이 세축이 종속적일 수 밖에 없는데,
( 이부분이 매우 중요하다. 세축이 종속적이기 때문에 짐벌 락이라고 표현함 )
z축을 돌리는 순간 x,y축은 함께 돌기 때문이다.
손가락으로 좌표계를 만들고 엄지를 기준으로 돌려보면 검지랑 중지도 같이 돈다.
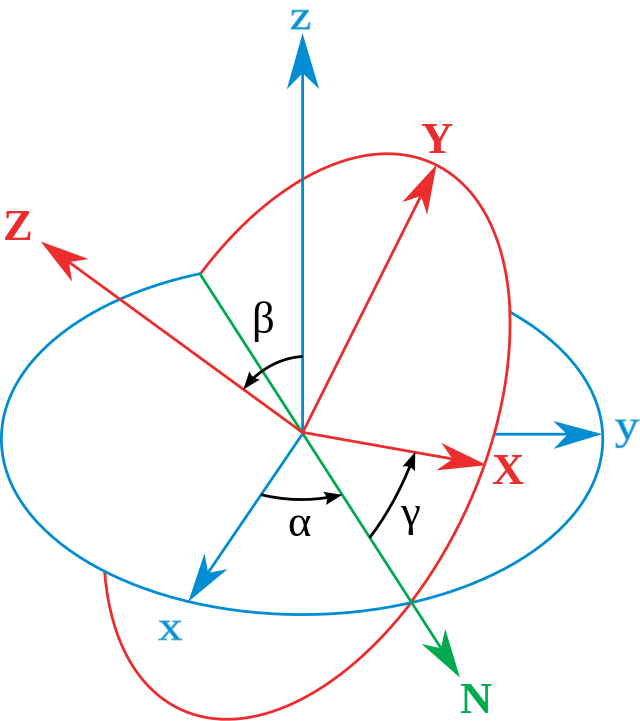
다른 방식으로 좀 더 자세하게 말하자면 위 그림에서 알파 베타 감마라는 임의의 회전각의 기준축은 다음과 같다
alpha: z-축(파란색)을 회전축으로 하여 회전된 x-y 좌표축의 각도
beta: 회전된 x-축(즉, N-축, 녹색)을 회전축으로 하여 회전된 z-y 좌표축의 각도
gamma: 위에서 회전된 z-축(즉, Z축, 빨간색)을 회전축으로 하여 회전된 x-y 좌표축의 각도
[출처 - 위키]
아래 그림이 이 현상을 표현하고 있다

짐벌락이란 이 세개의 각 중 beta의 범위가 제한적인 것을 말한다.
두번째 회전축이 돔에 따라서 첫번째 회전축은 가만히 있는데 세번째 회전축이 따라 돌기 때문에,
첫번째 회전축과 세번째 회전축이 겹쳐버리지 않게 하기 위해서다.
이렇게 오일러 각은 강체의 자세를 좌표축의 회전으로 표현하는 여러 방법 가운데 하나로
회전축의 순서에 따라 Z-X-Z 좌표라고도 불리기도 한다고 한다.
앞서 말한 x,y,z축을 기준으로 회전하는 것은 요 피치 롤 방식으로 X-Y-Z 좌표라고 한다고 한다.
여튼 이 두개는 조금 달라 보이긴 하지만 어쨌든 세개의 축이 종속적이며 단일 축에 대한 회전들로 강체의 방향을 표현하기 때문에 거의 비슷하다고 할 수 있다.
그런데 여기서 한가지 의문점이 든다.
왜 세축은 종속적일까?
왜 z축이 도는데 x,y축이 따라 돌까?
왜 3차원 공간에서의 회전이 짐벌에 비유되나?
3. 세 축이 회전에서 종속적인 이유
이 세축이 회전에서 종속적인 이유는 바로 오일러 각에서 회전 자체를 이 세 축으로 나눠서 계산하기 때문이다.
수학적으로 표현된 강체를 돌리기 위해서 우리는 세 축으로 회전 방향을 디지털화 시켰다.
x에 대해서 회전하고 y에 대해서 회전하고 z에 대해서 회전시켰다고 생각해보자.
a는 x에 대해서 회전시키면 이미 x로 회전된 a' 의 상태이고 우리는 a에 대해서 y축으로 회전하는 것이 아니라 a' 에 대해서 y축으로 회전하는 것이기 때문에 a"가 된다. 그리고 마지막으로 z에 대해서 회전시킬 때에는 이미 우리가 알던 a가 아니라 a"에 대해서 회전시키는 것이다.
이미 y축으로 돌릴 차례에는 x로 돌아간 상태이기 때문에 두 축에 대한 계산이 독립적일 수가 없다.
회전 변환 행렬을 곱할 때에 x에 대한 회전행렬 Rx가 있고 y에 대한 회전행렬 Ry가 있고 z에 대한 회전행렬 Rz가 있을때에
X라는 물체에 대해 회전을 시킨다면
RzRyRxX 와 같이 계산을 할 것이다.
(행렬의 곱셈 참고)
그런데 여기서 각 행렬은 서로 곱해지며 의존적으로 변하기 때문에 아무리 세축에 독립적으로 강체를 돌려보려 해도 그렇게 할 수가 없다.
그러면 xyz순이 아니라 yzx로 한다면?
이미 xyz xzy yzx yxz zxy zyx 순의 회전 변환에서 모두 짐벌락이 발생한다는 것이 증명되었다.
직관적으로 이것은 당연하다..!
세 축에 대한 회전때문에 발생하는 짐벌락을 피하기 위해서는 특정한 축에 대한 회전을 시도하거나, 쿼터니언을 통해 회전시키면 된다.
(특정한 축에 대해서 회전하려면 일단 내가 원하는 특정한 축을 기저의 어떤 한 축에 맞추는 회전변환 R을 시도하고, 맞춘 기저에 대해서 원하는 만큼 회전시키고, 첫번째로 시도했던 회전변환 R의 역행렬을 곱해주면 된다)
4. 짐벌락 현상이란
여기까지 이해했다면 짐벌락 현상이 무엇인지 동영상 한편을 보면 된다.

https://www.youtube.com/watch?v=zc8b2Jo7mno
이 동영상이 짐벌락 현상을 쉽게 설명해 주고 있다.
결론적으로 짐벌락이란
두번째 고리가 도는 것 때문에 첫번째 고리와 세번째 고리가 겹쳐지면, 첫번째 고리와 세번째 고리의 회전이 겹쳐져 버리기 때문에 한 축에 대한 자유도를 상실하게 된다. 그래서 두번째 고리를 움직일 때에 조심스러울 수밖에 없는데 이것이 바로 짐벌락 현상이다.
아폴로 11호는 이 짐벌락 현상 때문에 자세 제어에 어려움이 있었다고 한다.
그리고 옛날에 비행 시뮬레이터 같은 것들은 90도가 되는 것을 피하기 위해 89도 라던지 91도 라던지 살짝살짝 빗겨가게끔 코딩했다고 한다 ㅋㅋ
다행히도 우리에게는 쿼터니언이 있어서 이제 이런 어려움은 겪지 않아도 된다.
'computer science > 3d graphics' 카테고리의 다른 글
| 왜 정규화 벡터를 사용하는가 (0) | 2021.07.26 |
|---|---|
| OBB (Oriented Bounding Box)와 AABB (Axis-Aligned Bounding Box) (15) | 2021.07.26 |
| 동족좌표계와 동차좌표 (Affine Space, Homogeneous coordinate) (0) | 2021.07.26 |
| 컴퓨터 그래픽스 렌더링 파이프라인의 개요 (0) | 2021.07.26 |



댓글